sinx is odd or even|is cos odd : Tagatay Even and odd functions are classified on the basis of their symmetry relations. Even and odd functions are named based on the fact that the power function f (x) = x n is an even function, if n is even, and f (x) is an .
SERP Checker Analyze top-ranking pages and SERP features for any keyword. site Traffic Checker Enter a domain and explore all of the traffic sources. . Free Tools. Keyword Research Tool .
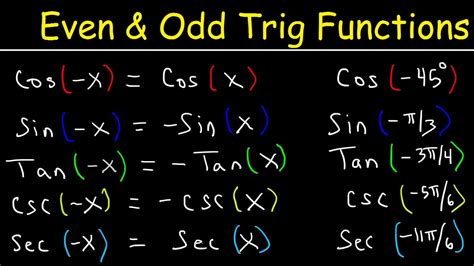
sinx is odd or even,graph {x^2 [-10, 10, -5, 5]} f ( −x) = −f (x) the function is odd. E.G. graph {x^3 [-10, 10, -5, 5]} If f ( −x) ≠ f (x) or f ( −x) ≠ − f (x) the function is not even or odd. Now the answer you need: the function y = sinx is odd, because sin( − x) = − sinx. graph {sinx [ .Precalculus. Determine if Odd, Even, or Neither f (x)=sin (x)cos (x) f (x) = sin(x)cos (x) f ( x) = sin ( x) cos ( x) Find f (−x) f ( - x). Tap for more steps. f (−x) = −sin(x)cos(x) f ( - x) = - .Trigonometric Even and Odd Functions. Applications and Examples. See Also. Trigonometric Even and Odd Functions. The cosine and sine functions satisfy the following properties: \begin {aligned} \cos (-\theta) .A function is said to be even if \(f(−x)=f(x)\) and odd if \(f(−x)=−f(x)\). Cosine and secant are even; sine, tangent, cosecant, and cotangent are odd. Even and odd properties can be used to evaluate trigonometric functions.is cos oddThey are called "odd" because the functions x, x 3, x 5, x 7, etc behave like that, but there are other functions that behave like that, too, such as sin (x): Sine function: f (x) = sin (x) It is an odd function. But an odd exponent .Even and odd functions are classified on the basis of their symmetry relations. Even and odd functions are named based on the fact that the power function f (x) = x n is an even function, if n is even, and f (x) is an . No, not all $\sin(f(x))$ are odd. In fact, you need $f$ to be odd for that to happen. Well, not exactly; the non-injectiveness of the sine function means there are .
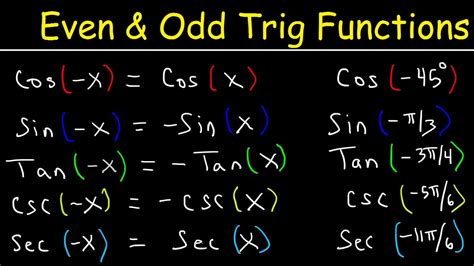
Find sin (-x) If sin(x) = .25, find sin( − x) Since sine is an odd function, sin( − θ) = − sin(θ). Therefore, sin( − x) = − sin(x) = − .25. 3. Find cos (-x) If cos(x) = .75, find .Example 1: Determine algebraically whether the given function is even, odd, or neither. [latex]f\left ( x \right) = 2 {x^2} – 3 [/latex] I start with the given function [latex]f\left ( x \right) = 2 {x^2} – 3 [/latex], plug in the value .Determine if Odd, Even, or Neither f(x)=(sin(x))/x. Step 1. Find . Tap for more steps. Step 1.1. Find by substituting for all occurrence of in . Step 1.2. Since is an odd function, rewrite as . Step 1.3. Dividing two negative values results in a positive value. . The function is even. The function is even. Step 3Determine if Odd, Even, or Neither f(x)=sin(x) Step 1. Find . Tap for more steps. Step 1.1. Find by substituting for all occurrence of in . Step 1.2. Since is an odd function, rewrite as . Step 2. A function is even if . Tap for more steps. Step 2.1. Check if . Step 2.2. Since , the function is not even.
Sine function: f(x) = sin(x) It is an odd function. . Don't be misled by the names "odd" and "even" . they are just names. and a function does not have to be even or odd. In fact most functions are neither odd nor . thus xsinx is an even function. This is graph of xsinx. Note symmetry about y-axis. even function >To determine wether a function is odd/even apply the following. • If f (x) = f ( -x) , then f (x) is even Even functions are symmetrical about the y-axis. • If f ( -x) = - f (x) , then f (x) is odd Odd functions have symmetry about the origin.The sine function and all of its Taylor polynomials are odd functions. The cosine function and all of its Taylor polynomials are even functions.. In mathematics, an even function is a real function such that () = for every in its domain.Similarly, an odd function is a function such that () = for every in its domain.. They are named for the parity of the powers of the .How to Determine if a Function is Even, Odd or Neither. I have prepared eight (8) worked examples to illustrate the procedure or steps on how to figure out if a given function is even, odd, or neither. The math involved in the calculation is easy as long as you are careful in every step of your solution.
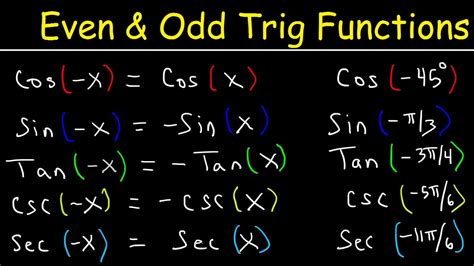
According to even-odd identity of sine function, the sine of negative angle is equal to negative sign of sine of angle. sin. . ( − θ) = − sin. . θ. This negative angle trigonometric identity of sine function can be proved geometrically in mathematical form.
To be odd, the function must obey: f ( −x) = −f (x) In this case, F ( −x) = sin( −x) +cos( −x) = −sin(x) + cos(x) F ( −x) ≠ F (x) or −F (x) hence it is neither even or odd. Answer link. It is neither. To be even the function must obey: f (-x) = f (x) To be odd, the function must obey: f (-x) = -f (x) In this case, F (-x) = sin .Determine if Odd, Even, or Neither f(x)=sin(3x) Step 1. Find . Tap for more steps. Step 1.1. Find by substituting for all occurrence of in . Step 1.2. Multiply by . Step 2. . Since , the function is not odd. The function is not odd. The function is not odd. Step 4. The function is neither odd nor even. 1 Answer. f (x) = cos(x) ⋅ sin(x) is an odd function. Therefore, f (x) = cos(x) ⋅ sin(x) is an odd function. f (x) = cos (x)*sin (x) is an odd function. Recall that the definition of an even function is f (x) = f (-x) and the definition of an odd function is f (x) = -f (x) Let's check either of these properties for our function f (x) = cos .
Recall that cosine is an even function and sine is an odd function. In terms of equations: $$\cos(-x) = \cos(x)$$ $$\sin(-x) = -\sin(x)$$ We can determine whether each of the other basic trigonometric functions is even, odd, or neither, with just these two facts and the reciprocal identities. sin^2(x) is an even function. A function f(x) is even if f(-x)=f(x) and function is odd if f(-x)=-x. As f(x)=sin^2(x) f(-x)=sin^2(-x) = (sin(-x))^2 = (-sin(x))^2 .A function f is said to be an even function if for any number x, f(–x) = f(x). Most functions are neither odd nor even functions, but some of the most important functions are one or the other. Any polynomial with only odd . An even function is a function where the value of the function acting on an argument is the same as the value of the function when acting on the negative of the argument. Or, in short: f(x) = f( − x) So, for example, if f(x) is some function that is even, then f(2) has the same answer as f( − 2). f(5) has the same answer as f( − 5), and .Although even roots of negative numbers cannot be solved with just real numbers, odd roots are possible. For example: (-3) (-3) (-3)=cbrt (-27) Even though you are multiplying a negative number, it is possible to obtain a negative answer because you are multiplying it with itself an odd number of times. Let's walk through it a little more slowly:
sinx is odd or even is cos oddExample 1: Identify whether the function f(x) = sinx.cosx is an even or odd function.Verify using the even and odd functions definition. Solution: Given function f(x) = sinx.cosx.We need to check if f(x) is even or odd. We know that .
Tour Start here for a quick overview of the site Help Center Detailed answers to any questions you might have Meta Discuss the workings and policies of this siteA function f is odd if f (− x) = − f (x) Since sin ( − x ) = − sin x , it implies that sin x an odd function. That is why for example a half range Fourier sine series is said to be odd as well since it is an infinite sum of odd functions.
sinx is odd or even|is cos odd
PH0 · sin of zero
PH1 · is sin odd
PH2 · is cos odd or even
PH3 · is cos odd
PH4 · is 30 a even number
PH5 · is 0 even or neither
PH6 · even odd or neither calculator
PH7 · Iba pa